Kỹ năng giải bài toán thể tích, khoảng cách khối đa diện, khối tròn xoay

Những chia sẻ của thầy rất hữu ích, đặc biệt khi môn Toán được thi theo hình thức trắc nghiệm khách quan.
Kỹ năng dựng hình
Với kỹ năng dựng hình, thầy Trịnh Tuấn cho biết, bài toán trắc nghiệm thường hình vẽ không phức tạp, học sinh cần dựng hình nhanh và chuẩn theo các yêu cầu sau:
Dựng đa giác đáy, chân đường cao tùy theo từng loại; dựng đường cao theo hướng thẳng đứng từ đỉnh xuống mặt đáy; dựng các cạnh bên, các góc giữa cạnh với mặt, mặt với mặt.
Lưu ý chú thích tất cả các yếu tố bài toán đã cho, ví dụ như: Đánh dấu các cạnh bằng nhau,các góc bằng nhau, các góc vuông...ghi số đo các cạnh và góc đã cho hoặc suy ra được từ tính chất các đa giác đặc biệt).
Đặc biệt, cần rèn luyện học sinh kĩ năng dựng góc một cách thành thạo (Đa phần đều dựa vào đường cao để suy ra hình chiếu các cạnh, từ đó suy ra góc)
Kỹ năng tính diện tích đáy và đường cao
Ngoài các hình mà công thức diện tích trong hình phẳng (Tam giác thường, tam giác đều cạnh a, tam giác vuông, tam giác vuông cân (nửa hình vuông), nửa tam giác đều, tam giác cân, hình chữ nhật, hình thoi, hình vuông, hình bình hành, đường tròn, hình thang), thầy Trịnh Tuấn đồng thời lưu ý một số trường hợp đáy bị chia nhỏ thành nhiều tam giác,hoặc bị cắt ra từ một đa giác khác dẫn đến việc tính diện tích trực tiếp trở nên khó khăn hơn.
Trường hợp này, có thể dùng tổng hoặc hiệu các đa giác khác để tính gián tiếp, hoặc dựa vào tỉ số đường cao, tỉ số cạnh đáy để tính diện tích.
Đường cao bao giờ cũng kết hợp với một cạnh ở mặt đáy (đi qua chân đường cao) tạo thành một tam giác vuông, ta chọn một tam giác vuông thích hợp (có ít nhất 2 cạnh, hoặc 1 cạnh 1 góc đã xác định) để tính đường cao.
Có khi đường cao còn được tính gián tiếp bởi công thức: h = 3V/B (đối với khối chóp)
Kỹ năng xác định và tính khoảng cách
Khoảng cách từ chân đường vuông góc đến 1 mặt phẳng: Theo thầy Trịnh Tuấn, đây là kĩ năng cơ bản nhất trong bài toán khoảng cách, đa phần các bài toán khác như: khoảng cách từ 1 điểm bất kì đến 1 mặt phẳng, khoảng cách giữa 2 đường thẳng chéo nhau đều có thể liên kết về chân đường vuông góc để tìm khoảng cách.

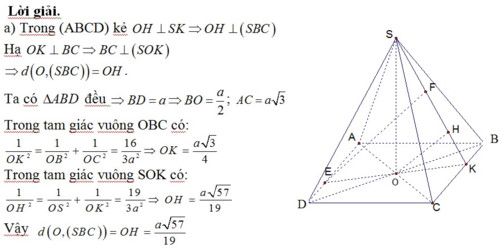
Khoảng cách từ 1 điểm bất kì thuộc mặt đáy đến 1 mặt phẳng: Kẻ đoạn thẳng từ điểm ấy qua chân đường vuông góc đến cắt mặt phẳng đang xét tại một điểm, tính tỉ số độ dài các đoạn thẳng từ đó suy ra tỉ số khoảng cách.
Khoảng cách giữa 2 đường thẳng chéo nhau: Từ đường thẳng này tìm hoặc kẻ đường thẳng song song với đường thẳng kia đưa về dạng khoảng cách giữa 1 đường thẳng song song với 1 mặt phẳng, đó cũng là khoảng cách từ một điểm bất kì thuộc đường thẳng đến mặt phẳng (Xem mục X và ví dụ c):
Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng: d(M,a) = MH; d(M,(P)) = MH. Trong đó, H là hình chiếu của M trên a hoặc (P).
Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song: d(a,(P)) = d(M,(P)) trong đó M là điểm bất kì nằm trên a. d((P),(Q)) = d(M,(Q)); trong đó M là điểm bất kì nằm trên (P).
Khoảng cách giữa hai đường thẳng chéo nhau: Đường thẳng delta cắt cả a, b và cùng vuông góc với a, b được gọi là đường vuông góc chung của a, b. Nếu delta cắt a, b tại I, J thì IJ được gọi là đoạn vuông góc chung của a, b. Độ dài đoạn IJ được gọi là khoảng cách giữa a, b.
Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó với mặt phẳng chứa đường thẳng kia và song song với nó.
Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
Các kiến thức cơ bản cần ghi nhớ
Tỷ số góc nhọn trong tam giác vuông:

Hệ thức lượng trong tam giác vuông:
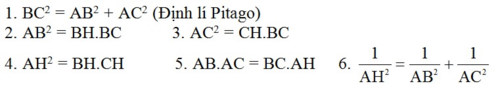
Định lí Côsin:
Định lí Sin:
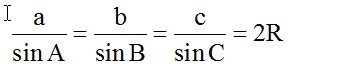
Định lí Talet:
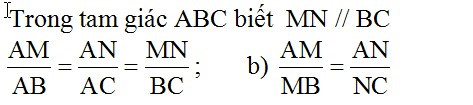
Diện tích trong hình phẳng:





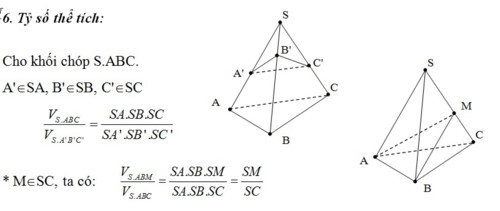
Đường cao trong hình chóp, lăng trụ và hình tròn xoay:
Đường cao hình chóp: Chóp có cạnh bên vuông góc với đáy, đường cao chính là cạnh bên ấy. Chóp có hai mặt bên vuông góc đáy, đường cao là giao tuyến của hai mặt bên vuông góc đáy.
Chóp có mặt bên (hoặc mặt phẳng có chứa đỉnh) vuông góc đáy, đường cao nằm trong mặt bên (hoặc mặt phẳng có chứa đỉnh) vuông góc với đáy tại giao tuyến.
Chóp đều, đường cao từ đỉnh đến tâm đa giác đáy. Chóp có hình chiếu vuông góc của một đỉnh xuống mặt đáy thuộc một cạnh của mặt đáy, đường cao là từ đỉnh tới hình chiếu.
Đường cao của lăng trụ: Lăng trụ đứng, đường cao là cạnh bên. Lăng trụ xiên, đường cao từ một đỉnh tới hình chiếu của nó thuộc một cạnh nằm trong mặt đáy.
Đường cao của hình nón: Từ đỉnh đến tâm đường tròn đáy.
Đường cao của hình trụ: Đường nối tâm của 2 đường tròn đáy (hoặc đường sinh).
Góc:
Góc giữa hai đường thẳng đưa về góc nhọn giữa hai đường thẳng cắt nhau. Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó lên mặt phẳng.

Góc giữa hai mặt phẳng cắt nhau là góc giữa hai đường thẳng lần lượt vuông góc với giao tuyến của hai mặt phẳng đó tại một điểm:
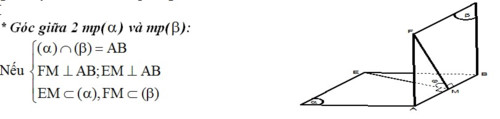
Khoảng cách:

Một số bài tập trắc nghiệm minh họa
Dưới đây là một số bài tập trắc nghiệm minh họa được thầy Trịnh Tuấn giới thiệu:






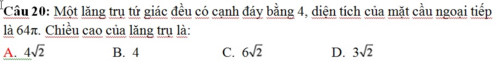
Hy vọng với những chia sẻ trên đây của AZtest sẽ giúp quý thầy cô có thể cung cấp cho học sinh của mình những kỹ năng giải bài toán thể tích, khoảng cách khối đa diện, khối tròn xoay.
>>>Xem thêm: Cách tạo đề thi trắc nghiệm Toán hình học: Khái niệm khối đa diện
ĐỪNG QUÊN ĐỂ LẠI EMAIL CUỐI BÀI ĐỂ NHẬN THÊM NHỮNG THÔNG TIN HẤP DẪN CỦA AZTEST
---------------------------------------------------------------------------------------------------------
AZtest là hệ thống tạo lập website thi trắc nghiệm trực tuyến do CÔNG TY TNHH PHÁT TRIỂN VÀ DỊCH VỤ NGUỒN MỞ THUẬN ĐỨC phát triển. Với AZtest, người dùng có thể dễ dàng sở hữu một website tổ chức ôn tập, thi trắc nghiệm trực tuyến hoàn toàn miễn phí, độc lập, được cá nhân hóa theo yêu cầu của người quản trị.
Liên hệ hotline 02337774455 hoặc Fanpage https://m.me/aztest.vn để được tư vấn trực tiếp bởi đội ngũ kỹ thuật viên của AZtest.
Hải Bình
Nguồn tin: Báo Giáo dục và thời đại
Những tin mới hơn
Những tin cũ hơn




